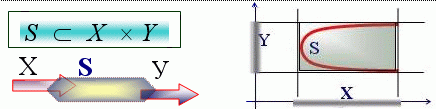
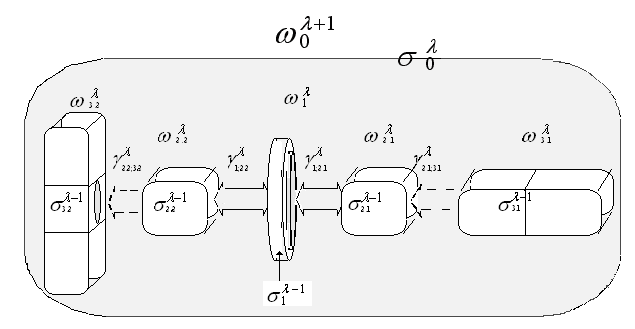
__________________
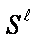 is described by following symbol
construction:
is described by following symbol
construction:
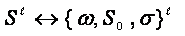
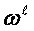 - aggregated dynamical realization of the units and acts,
- aggregated dynamical realization of the units and acts,
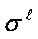 - construction,
- construction, 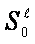 -
co-ordinator,
-
co-ordinator, 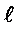 - index of level,
- index of level, 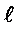
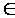
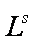 .
.
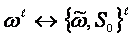 ,
, 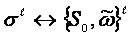 ,
,
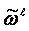 and
and
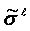 are connected by
are connected by 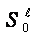 and
contain the dynamical realizations and constructions of unit (object)
and
contain the dynamical realizations and constructions of unit (object) 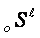 , its environment
, its environment 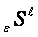 (other units of its level), acts
(processes)
(other units of its level), acts
(processes) 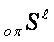 of
of 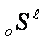 in
in
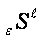 and acts
and acts 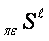 of
of
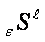 with
with 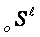 :
:
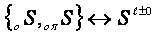 ,
, 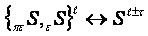 ;
;
that is level 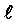 is
discovered in the interlevel connections:
is
discovered in the interlevel connections:
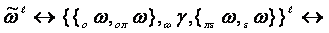
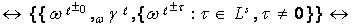
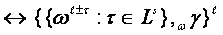
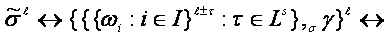
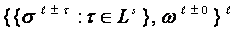 .
.
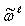 contains the dynamical systems
contains the dynamical systems
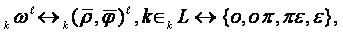
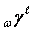 - connections of
- connections of 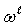 with
other units and acts, and the construction of
with
other units and acts, and the construction of 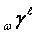 connects
the details of
connects
the details of 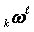
(their states 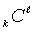 , inputs
, inputs 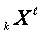 and outputs
and outputs 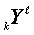 ):
):
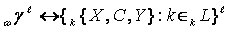 .
.
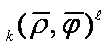
The network of
connections of 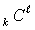 ,
,
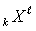 ,
, 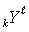 is
described by Table 1. As can be seen,
is
described by Table 1. As can be seen, 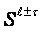
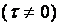 has details, which have
increasing uncertainty in the signs of
has details, which have
increasing uncertainty in the signs of 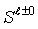 ;
;
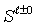 sets
sets 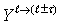 and gets
and gets
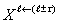 - outputs of level
- outputs of level 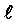 to the
lower
to the
lower 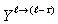 and
higher
and
higher 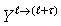 levels and inputs from levels
levels and inputs from levels 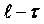 and
and 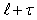 (
( 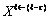 ,
,
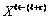 ); states
); states 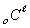 are own inputs and outputs of level
are own inputs and outputs of level 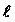 :
: 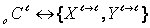 Thanks to the
connections in
Thanks to the
connections in 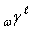 any detail of
any detail of 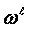 is restored by its other details with becoming
uncertainty:
is restored by its other details with becoming
uncertainty:
Table 1
The co-ordinator is
described by the following way:
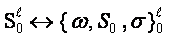 ,
,
that is 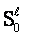 has own
aggregated dynamical realization
has own
aggregated dynamical realization 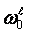 and the
construction
and the
construction 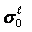 ; the availability of
; the availability of 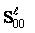 (the
connection with higher levels) allows to account and to change
(the
connection with higher levels) allows to account and to change 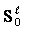 by its own activity.
by its own activity.
Let 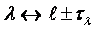 ,
, 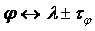 ,
, 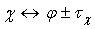 ,
,
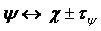 ,
, 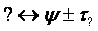 ,
etc.,
,
etc., 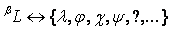 .
Then
.
Then 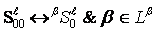 ;
;
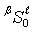 is the contraction of field
is the contraction of field 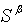 on the
on the
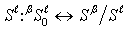 and
and
The fields 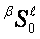 are
strata of
are
strata of 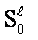 and
and 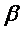 is
outlook in the level space. The knowledge uncertainty of
is
outlook in the level space. The knowledge uncertainty of 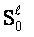 is
increased with the distance from
is
increased with the distance from 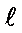 . Every
level
. Every
level 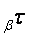 of uncertainty on every stratum
of uncertainty on every stratum 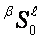 has its own coordinating strategy. The strategies of
has its own coordinating strategy. The strategies of 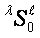 (processes
(processes 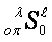 ) connect the changes of constructions
) connect the changes of constructions
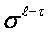 and
and 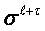 with the
using of
with the
using of 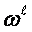 . The act of key unit
. The act of key unit 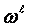 creation
in
creation
in 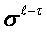 is uniting process, the act of
is uniting process, the act of 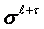 creation when
creation when 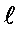 is the highest level is the multiplying process
with the initial unit
is the highest level is the multiplying process
with the initial unit 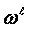 .
.
__________________________________________________________________
References
prg1. Novikava S., Miatliuk K.,Ananich G.,Mazanik L.,Gancharova S.,
Galavenchik I., Suponitsky W. The Theoretical Model and the Application of
Aed-processor. The International Symposium on Neural Networks and Neural
Computing, NEURONET'90, Prague, pp. 259-261.(Reprinted by World Scientific
Publishing Co., under the title "Theoretical Aspects of Neurocomputing", Vol.1,
Singapore, 1991).
net1. S.Novikava, K.Mialtiuk,
S.Gancharova, W.Kaliada, A.Ivanov, S.Kritsky, A.Demyanenka, A.Zhybul. Aed
Theory and its Realizations by Hierarchical Knowledge Networks. Preprints of
the IFAC Conference on Supplementary Ways for Improving International Stability
- SWIIS'95, Vienna, Austria, 1995, p.99-106.
net2. S.Novikava, K.Miatliuk,
S.Gancharova, A.Ivanow, A.Zhybul, A.Danichaw, P.Buka, V.Siageichick. Aed
Theory and Hierarchical Knowledge Networks. Proceedings of the Annual
Conference of ICIMS-NOE (E.P.9251) on ASI'96 in Life Cycle Approaches to
Production Systems: Management, Control, Supervision. Toulouse, France, 1996,
p.377-386.
net3. S.Novikava, S.Gancharova,
A.Burawkin, S.Daronin, P.Buka, A.Ivanow, A.Danichaw, A.Demianenka, M.Maroz,
A.Michalevich, A.Zagaradnuk. Mathematical Defining of Sway Networks of State
and States Unions. Preprints of Eleventh International Conference on
Mathematical and Computer Modeling and Scientific Computing. Washington, DC,
USA. 1997. p.150.
dem1. W.Nowik, V.Barkalin,
W.Zianevich, S.Gancharova, P.Buka, K.Miatliuk, A.Astrowskaya, A.Bahutski,
Demographic Units in Hierarchical Coordinates: Construction, Activity and
Goals, Preprints of the IFAC Conference on Supplementary Ways for Increasing
of International Stability - SWIIS'95, SWIIS'98, Sinaia, Romania,
1998.
econ1. P.Groumpos, S. Novikava,
S. Gancharova, A.Zhybul, V. Siarheichyk, K.Miatliuk,. Design&Creating of
New Engineering Units in Reconstruction Regions. Proceedings of the Annual
Conference of ICIMS-NOE (E.P.9251) on ASI'97 in Life Cycle Approaches
bio1. Novikava S.I.,Miatliuk
K.N., Gancharova S.A.,Ananich G.A., Novik V.A., Koleda V.V., Kavalyov V.A.,
Boika T.N. Aed Technology for Ecological, Social and Engineering Systems
Coordination. Proceedings of Eighth International Symposium on Modular
Information Computer Systems and Networks, ICS-NET'91, Dubna, pp.
145-152.
bio2. V.Kaliada, V.Rabeka,
Iu.Kaminski, E.Kaminskaia. Oncological Defense Maintenance in Dynamic
Multilevel Environment. IXth International Conference on Mathematical and
Computer Modelling, ICMCM'93, Berkeley, California, USA, p. 128.
phys1. Bagnich S. and Konash
A. Computation Study of the Percolation Phenomena in Inhomogeneous Two- and
Three- Dimensional systems. J. Phys. A: Math. Gen.36 (2003) 1-13,
phys2 Bagnich S. and Konash
A Percolation processes in heterogeneous two-dimensional space Phys.
Solid State 42 (2002) 1775.
phys3. Pavel Buka, The
Investigation of Photoluminescence in Low-Dimensional Materials with
Aed-Processor. The Eleventh International Conference on Superlattices,
Microstructures and Microdevices. Book of Abstracts. Hurghada (Red Sea), Egipt,
July 27- August 1, 1998
_______________________________________________________________________________________
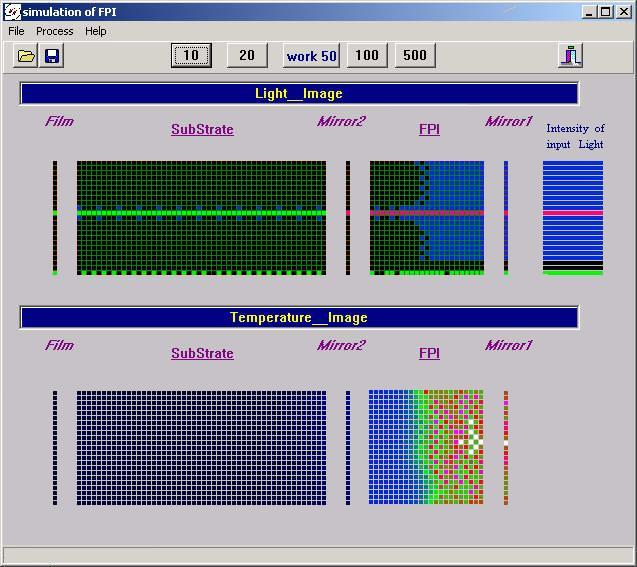
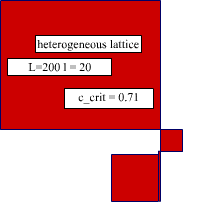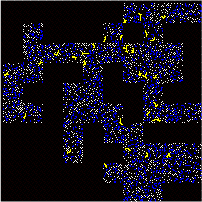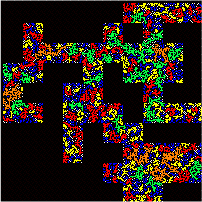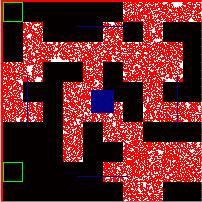
Simulations